So yesterday was all math, and today was all education. …well sort of. Academic artists have a world view that is quite different from that of your typical scientist. I come from a very analytic background. Even my hobbies, playing poker and racing cars, and my artistic work in photography are a blend of the creative and the analytic. Once I wrapped my brain around the different way in which they were looking at the problem of pedagogy, there were some good take-away points from the morning and afternoon sessions.
One of the things that true of both artist and scientist is that we fail, and I mean we fail a lot. Most of our careers is spent creating one failure after another. This is NOT a bad thing, unless it’s the only thing you’re doing. The road to success is lined with a long sequence of failures, and those who do succeed accept this and even embrace it. When students finally arrive in a college classroom, they are absolutely terrified of failure. Personal note: This should not be a surprise given how frequently we subject our kids to high-stakes standardized testing, but that’s a topic for another article. Game development, much like the development of a new scientific model, is a process of constant iteration. You try, test, fail, tweak, test, fail, rinse and repeat. So many of our students are fearful of that initial failure that they don’t even attempt the work and fail in a far more destructive way. Mitigating, navigating, and learning from failure through iteration is paramount in game development just as it is in science, but it’s a tough thing to teach.
There were more ideas that I picked up throughout the day, but nothing really groundbreaking. I have some ideas related to the iteration process and managing failure I mentioned above that I will craft into some new exercises for the Astronomy courses. I’ll have more on that as I develop the idea into more than just thoughts in my head.
The last talk I attended was by Margaret Moser, “Teaching Designers to Code”. I thought that this would be useful not only because we occasionally get a more design-focused student in the Math and Physics for Games course, but also because even many of the programming-focused students are really just learning how to code efficiently. The two big take-away items here were not ones that were startling revelations, but rather stern reminder of what I already knew and should be deploying in my classroom. Something I could do better when describing algorithms in class is not to start writing line-items of pseudo code or equations, but instead to start with a block diagram of the process. This, of course, is the key to coding more complex solutions. Don’t think in terms of individual lines, but think in terms of functional blocks. That’s how I think of my scientific work. Think about the big blocks of the problem before you drill down into writing specific equations.
 The evening ended brilliantly. Professor Hanna and I made our way down to a region where my good friend and fellow photographer, Bash Beard, took me when I was in town for the AGU Fall Meeting, Beldon Place. At first, it just looks like a sketchy back alley, but when you peek around the corner, it’s lined with one amazing restaurant after another with just about every type of food you can think to eat. We tried the last restaurant at the end of the alley, Brindisi Cucina Di Mare. Of course I was going to sniff out a seafood joint. What else did you expect?
The evening ended brilliantly. Professor Hanna and I made our way down to a region where my good friend and fellow photographer, Bash Beard, took me when I was in town for the AGU Fall Meeting, Beldon Place. At first, it just looks like a sketchy back alley, but when you peek around the corner, it’s lined with one amazing restaurant after another with just about every type of food you can think to eat. We tried the last restaurant at the end of the alley, Brindisi Cucina Di Mare. Of course I was going to sniff out a seafood joint. What else did you expect?
Tomorrow is the first day of the main conference which means SWAG!!! The Expo Hall opens and it’s time to meander around the vendor booths and see what kind of cool loot I can drag back for my students, for Lillian, and for my officemate’s geocaches. It’s also the day of the Game Developers Choice Awards. Think the Oscars for video games, only with a bit more edge to it.



 What to do while in the Powell and Market area and your stressed out? Eat! Senior Scientist at Fundamental Technologies, Jerry Manweiler, introduced me to a great burger joint on Union Square, the Burger Bar. Wet, stressed, and hungry, That’s where Russ and I went. It’s an amazing place with an amazing view, although I will say the view during the Christmas season when I come here for the American Geophysical Union Fall Meeting is a bit more colourful.
What to do while in the Powell and Market area and your stressed out? Eat! Senior Scientist at Fundamental Technologies, Jerry Manweiler, introduced me to a great burger joint on Union Square, the Burger Bar. Wet, stressed, and hungry, That’s where Russ and I went. It’s an amazing place with an amazing view, although I will say the view during the Christmas season when I come here for the American Geophysical Union Fall Meeting is a bit more colourful. 

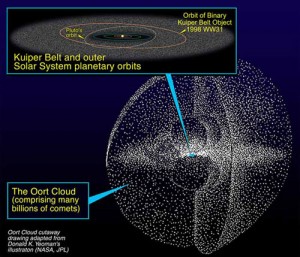 This places its perihelion around 280 AU. That’s really far out there, and places the proposed object as a member of the distant Kuiper Belt or inner Oort Cloud, or Hills Cloud, rather than a member of the inner Kuiper Belt wherein resides more familiar objects like Pluto and Eris. The mathematics are extremely compelling and the discussion and conclusions well-reasoned, but as the modern saying goes, “Pics or it didn’t happen.”
This places its perihelion around 280 AU. That’s really far out there, and places the proposed object as a member of the distant Kuiper Belt or inner Oort Cloud, or Hills Cloud, rather than a member of the inner Kuiper Belt wherein resides more familiar objects like Pluto and Eris. The mathematics are extremely compelling and the discussion and conclusions well-reasoned, but as the modern saying goes, “Pics or it didn’t happen.” 