In January, right at the beginning of the Spring semester, Professor of Planetary Astronomy Michael Brown and Assistant Professor of Planetary Astronomy Konstantin Batygin, both from the California Institute of Technology, published a remarkable prediction in the Astronomical Journal, Evidence for a Distant Giant Planet in the Solar System (read the article here, http://web.gps.caltech.edu/~kbatygin/Publications_files/ms_planet9.pdf) In the article, Dr. Batygin, the theoretician of the pair, uses Dr. Brown’s observations of objects within the Kuiper Belt to argue for the existence of an object in a Sedna-like orbit and approximately ten times the mass of Earth. The basis for their claim is the ordered clustering of the perihelions of the orbits of multiple Kuiper Belt objects, a phenomenon that has a 0.007% of occurring randomly (yes, the significance of the number was not lost on me). After a significant amount of modelling and numerical analysis, Dr. Batygin predicts the likely orbital parameters of the Neptune-sized object as being inclined as much as 40 degrees to the ecliptic and having a semi-major axis of ~700 AU with an eccentricity of ~0.6. 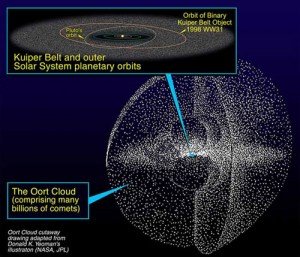 This places its perihelion around 280 AU. That’s really far out there, and places the proposed object as a member of the distant Kuiper Belt or inner Oort Cloud, or Hills Cloud, rather than a member of the inner Kuiper Belt wherein resides more familiar objects like Pluto and Eris. The mathematics are extremely compelling and the discussion and conclusions well-reasoned, but as the modern saying goes, “Pics or it didn’t happen.”
This places its perihelion around 280 AU. That’s really far out there, and places the proposed object as a member of the distant Kuiper Belt or inner Oort Cloud, or Hills Cloud, rather than a member of the inner Kuiper Belt wherein resides more familiar objects like Pluto and Eris. The mathematics are extremely compelling and the discussion and conclusions well-reasoned, but as the modern saying goes, “Pics or it didn’t happen.”
This certainly isn’t the first time that an object has been predicted to exist by mathematical analysis of the orbit of other objects. The most famous, and earliest, is the prediction by French astronomer and mathematician Urbain Le Verrier of the existence of an eighth planet beyond the orbit of Uranus that would account for the Uranus’ increase and subsequent decrease in orbital speed unrelated to its solar distance. Le Verrier worked on the problem in the summer of 1846 during his position at the Paris Observatory. Using Newton’s mechanics and Law of Gravity and the observed positions of Uranus, he calculated where a more distant planet would have to be and how massive it would have to be to produce the observed deviations. After completing his work, two astronomers, Johann Gottfried Galle and Heinrich Louis d’Arrest at the Berlin University, began searching in the vicinity of Le Verrier’s predicted position for the new planet. Galle, looking through the telescope, called out positions and brightnesses of the visible objects to d’Arrest who compared the observations to previously recorded charts until Galle called out an object that was not on the chart. They had found the planet that would later come to be called Neptune within a single degree of Le Verrier’s calculations. It was a remarkable piece of work from both Le Verrier and from Galle and d’Arrest, and it was a triumph for Newtonian mechanics.
This method of discovering new objects was later attempted by William H. Pickering, Professor of Physics at Harvard University. Based on his calculations, using the apparent discrepancies in the orbits of both Uranus and Neptune, he attempted to image the proposed trans-Neptunian object at the Mount Wilson Observatory outside of Pasadena, CA. His search was unsuccessful, but the hunt for “Planet X” was picked up by Percival Lowell who had founded the Lowell Observatory in Flagstaff, AZ. Lowell’s attempts were equally unsuccessful. After Lowell’s passing, the search was tasked to an amateur astronomer from Burdett, KS, 23-year old Clyde Tombaugh. Rather than relying on sophisticated calculations, Tombaugh was tasked with systematically searching the Zodiac for anything non-stellar. In late January 1930, he captured two images of the object that we now know as Pluto. As it turns out the position of Pluto did not in any way correlate to Pickering’s calculations. In this case, the discrepancies were due to the lack of precision in the measurement of the masses of the outer planets.

Today, modern astronomers use the periodic motion of stars to mathematically infer the presence of extrasolar planets. The first of these discoveries was 51 Pegasi b. As two bodies orbit each other, such as a planet around its host star, the two bodies both move about their common center of mass. The planet being significantly less massive moves far more noticeably than the star, but the star does still move. Its motion is detectable by analysis of its light spectrum’s becoming alternately slightly bluer and then slightly redder as the star moves towards us and then away from us, respectively. This method has been used to locate many such extrasolar planets that we’re still unable to image directly. These are generally accepted as exceptions to the “Pics or it doesn’t exist” rule in science. The mathematics and analysis are so strongly compelling and there is no other viable alternate explanation that it is accepted that orbiting planetary bodies are responsible for the variations in the radial velocity of 51 Peg and other stars.
So now if we’re willing to take the mathematical word of the existence of extrasolar planets such as 51 Peg b, then why not for this new object proposed by Dr. Batygin and Dr. Brown from Cal Tech? The difference lies in the complexity of the problem. The extra solar planet problem is by comparison a simple problem. The radial velocity curve for 51 Peg is very clean, and the analysis of the data use methods that have long been vetted and refined by astronomers studying binary stars for which one can see the two separate objects. In other words, there is precedent for the methodology. This is not to say that Dr. Batygin’s methods are controversial or that the mathematical tools are not well understood. The Hamiltonian mechanics he deploys in his paper are extremely well understood and have been for over a century, but the data with which Dr. Batygin is working and the significant complexity created by moving from a two-body problem to an n-body problem make the analysis more difficult and intricate as well as making the results of those analyses less precise. For this reason, while I am very excited about this new prediction, I want to see an image before I take it as fact.
The observational discovery this new object, if it exists, likely won’t happen soon. Even at its proposed closest approach to the Sun, 280 AU, the intensity of sunlight striking the object is 0.00128% that of what it is here at Earth. Not only is the light very dim at that distance, most Kuiper Belt and inner Oort Cloud objects are coated with carbonaceous dust making their surfaces very dark and non-reflective. As our observational tools and techniques improve, we may eventually be able to start imaging these remote sentinels of our solar system, but until then, we’re left with only the predictions.
